- Kepler-16b was the Kepler telescope’s first discovery of a planet in a “circumbinary” orbit– circling two stars, as opposed to one star in a double-star system. Like Luke Skywalker's home planet Tatooine, Kepler-16b would have two sunsets if you could stand on its surface.
- Kepler’s First Law Describes the Shape of an Orbit The orbit of a planet around the Sun (or of a satellite around a planet) is not a perfect circle. It is an ellipse—a “flattened” circle. The Sun (or the center of the planet) occupies one focus of the ellipse.
Introduction
Since at least the time of Hipparchus and Eudoxus the ancient world believed that the Sun, moon, planets, and stars moved around the earth in circular orbits. Aristotle’s Physics put the heavenly bodies on perfect crystal spheres. This theory was further formalized in the second century by Ptolemy in his Almagestwhich served the basic needs of astronomers for the next 1,500 years. Over that time, Aristotelian physics became an article of faith not to be questioned.
But there were unexplained irregularities that never quite fit the theory. The ancients knew that the seasons were of different lengths. For example, Winter is about 89 days in length while Summer is about 94 days. Why did the Sun sometimes speed up and slow down like that? They also noticed that Mars would move East across the night sky for a few years, slow down, and then reverse course and move West for a few months before looping back to its original course. (What we now call apparent retrograde motion.)
Copernicus took a step forward by putting the Sun at the center of the universe but he still retained and tweaked Ptolemy’s epicycles. Tycho Brahe proposed a hybrid model in which the planets orbited the Sun but the Sun and Moon orbited the Earth. Yet he too retained the circular orbits. In his Epitome of Copernican Astronomy, Johannes Kepler summed up the quandary nicely:
The ancients wished it to be the office of the astronomer to bring forward such causes of this apparent irregularity as would bear witness that the true movement of the planet or spheres is most regular, most equal, and most constant, and also of the most simple figure, that is, exactly circular. And they judged that you should not listen to him who laid down that there was actually any irregularity at all in the real movements of these bodies (Book IV, 571).
So the problem came down to metaphysics. The circle was a symbol of perfection. And the heavens were the perfect creation of God. Who would suggest otherwise and earn the wrath of all Christendom? And yet Kepler ended up doing exactly that, finally proposing the ellipse as the figure the planets describe as they orbit the Sun. Kepler worked out a method (Kepler’s Equation) that determines where an orbiting body like the Earth is in its orbit around the Sun. That is the subject I’ll explore here.
The Problem
Kepler's 3rd Law calculator. G m t² = 4 π² r³. Kepler's 3rd Law Ultra Calculator Solves for Mass, Orbital Radius or Time Scroll to the bottom for instructions.
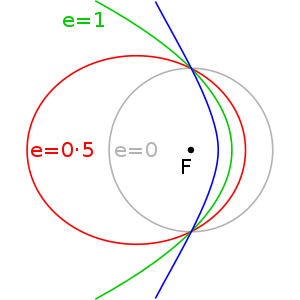
The version of Kepler’s Equation (KE) I’ll walk through works for any elliptical orbit in the interval [0, 1). That is to say where 0 <= e < 1 with 0 being a circle and 1 being a parabola. In the figure below we have an elliptical orbit of planet P. The eccentricity of the ellipse is greatly exaggerated for the purposes of illustration; Earth’s orbital eccentricity e is actually about 0.016 making it closer to a circle.
Of the two foci, the Sun S is shown at one focus and the other is empty. Planet P now at time t is moving counterclockwise and went through apsis A (perihelion) at time τ. What we want to know is where is P now at time t? To get there we have to explore three kinds of angles in orbital mechanics: the mean anomaly, the eccentric anomaly, and the true anomaly.
Properties of an Ellipse
Every ellipse has a center, two foci, and a major and minor axis. In the figure of the ellipse below I’ve labeled AB as the major axis and CD the minor axis. I’ve also labeled semi-major axis a and semi-minor axis b.
Earlier I said the eccentricity of the ellipse is going to be in the interval [0, 1). Its eccentricity is related to a and b by:
$$e=sqrt{1-leftlgroup b over a rightrgroup^2}$$
Mean Anomaly
Kepler’s second law tells us that “planets sweep out equal areas in equal times.” That is to say P does not move uniformly in its orbit. It speeds up at perihelion when it is closest to the gravitational pull of S and slows down when it is furthest away at aphelion. This irregularity is the main reason the problem is hard to solve.
But what if we set aside the elliptical motion for now and created a fictitious planet P’ moving at a constant speed in a uniform circular orbit? It would be easier to calculate that angle and then use it later to solve the real problem. In this diagram P’ moves in a circle around center C while the real planet P moves in an ellipse around focus S:
This mean (average) movement of P’ between any two points in time always sweeps out an equal area for any duration of time. The angle created is called the mean anomaly. In the figure above mean anomaly angle M is the interior angle of the area CP’A. Let T represent the time it takes for P’ to complete one orbit around S. For example, if P is the Earth then T = 365.256 days. So the radius vector CP’ sweeps counterclockwise from A to 2π (0 to 360 degrees) once in time T. At a given moment t we can determine M by:
$$M = {2 pi t over T}$$
We will need M later to solve KE. First, let’s look at a second angle called the eccentric anomaly that Kepler created as a stepping stone to get to the true anomaly.
Eccentric Anomaly
Here’s Kepler’s trick for creating a new angle he called the eccentric anomaly. As with angle M describe a circle whose diameter is equal to the ellipse’s major axis AB as in the figure below. In other words, the center of circle C is also the center of the ellipse. Draw a line segment perpendicular to AB that runs from R on up through P to the circle at point Q. Angle QCA is eccentric anomaly E. Angle PSA is the true anomaly ν. Angle E forms a relationship with angle ν as we shall see next.
True Anomaly
Note in the figure below that a is also the radius of the described circle. Angle ν is the true anomaly but I’ve now added the radius vector to the diagram. The radius vector (hypotenuse r in PSR) is the distance center-to-center measured in astronomical units (AU) between the Sun S and the planet P.
Now we see why Kepler described the circle with a diameter equal to the major axis of the ellipse:
$${b over a} = {PR over QR}$$

This section goes through the relationship between ν and E. If you’re not up for the trigonometry feel free to skip down to the last function (85). Otherwise following Smart (pp. 112-113) ( PR = r sin nu ) and (QR = CQ sin E) = ( a sin E) so:
$$r sin nu = b sin E tag{61}$$
And (SR = r cos nu ) so (SR = CR – CS = a cos E – ae) so:
$$r cos nu = a (cos E – e) tag{62}$$
$$r = a(1 – e cos E)$$
$$2r sin^2 {nu over 2} = r (1 – e cos E)$$
$$=a(1 – e cos E)-a(cos E – e) tag{63}$$
$$2r sin^2 = a (1 + e) (1 – cos E) tag{64}$$
$$2r cos^2 = a (1 – e) (1 + cos E) tag{65}$$
Dividing (65) into (64):
$$ tan^2 {nu over 2} = {1+e over 1-e} cdot {1- cos E over 1 + cos E}$$
$$ tan {nu over 2} = sqrt{1+e over 1-e} tan {E over 2}$$
Inverting so we can solve for ν:
$$nu = 2 arctan {leftlgroup sqrt{1+e over 1-e} tan {E over 2}rightrgroup}$$
Smart (p. 119) applies the formula for the logarithmic series to derive:
$$nu = E + (e + 0.25 e^3) sin E + 0.25e^2 sin 2E + 0.0833e^3 sin 3E tag{85}$$
Function (85) can easily be translated to programming code and solved if we know e and E. That’s where KE comes in.
Kepler’s Equation
Colwell (p. 3-4) walks through the derivation of KE. Area PSA = area PSR + area PRA. Then:
$$= {1 over 2} a (cos E – e)(r sin nu) + {b over a} Area QRA$$
$$= {1 over 2} ab (cos E – e)( sin E) + {b over a} leftlgroup {1 over 2} a^2 E = {1 over 2} a^2 sin E cos E rightrgroup$$
$$= {1 over 2} a^2 sqrt {1 – e^2} (E – e sin E)$$
Finally:
$$M = E – e sin E$$
Which I will put in the form:
$$E = M + e sin E$$
Where M is the mean anomaly angle, e is the ellipse’s eccentricity, and E is the eccentric anomaly angle. Because of (sin E) this is a transcendental equation. Therefore, we have to use an iteration method (or a series expansion) to solve for E. I am going to show two iteration methods, the first of which would have been familiar to Kepler. Once we have E we can get coordinates P(x,y) from:
$$x = a (cos E – e)$$
$$y = b sin E$$
Solving Kepler’s Equation
Now I’m going to convert the functions needed above into the C# programming language since I’m fluent in that. As with my previous posts on the subject I’m going to rely heavily on Meeus for the core algorithms as well as bit and pieces of functions from various Wiki articles. To keep it simple I’m just going to calculate the Earth’s orbit; however, the public source code available in my GitHub repository is structured such that you could add Mars or any other planet to the solution.
As detailed in a previous post I have a Moment struct that accepts any DateTime value and can return the Julian Day (JD) or the Time T in Julian centuries of 36525 ephemeris days from the J2000.0 epoch.

A second struct is named Earth which accepts a Moment value and calculates the necessary orbital elements for the Earth, its mean anomaly M and eccentricity e in particular. Following Meeus, to find M for a given moment we need the four coefficients for both Earth’s mean longitude L and the perihelion’s mean longitude P which I’ve implemented as a simple Dictionary:
I use the same implementation for eccentricity e:
Now that I have M and e I can solve KE. Meeus provides four methods. I implemented the first two and put some instrumentation around them to get a sense of their performance. The first method is a simple fixed-point iteration, which is what Kepler himself did to solve the equation. Let (E_0 = M) be the default value for E in the first calculation. Then take the output and pass it back into the equation a second time for greater accuracy:
$$E_1 = M + e sin E_0$$
$$E_2 = M + e sin E_1$$
$$E_3 = M + e sin E_2$$
and so on until the desired accuracy is reached. Kepler stopped at (E_2) because that was good enough in his day. But in my implementation of this first method I found it needed 120 iterations (taking 0.0928 ms) to achieve the desired accuracy:
The second method is much faster and produces the desired level of accuracy after only 5 iterations and 0.0059 ms:
Given e and E we can now calculate the true anomaly ν using equation (85) above:
And of course now that we have ν we can get the radius vector r:
Output
I ran the program for 9 PM this evening as of this writing (2019-04-07 21:00 UTC):
Now to check this output against JPL’s Horizons system:
Here’s the comparison between the three highlighted values against my output:
| Eccentricity e | Mean anomaly M (deg) | True anomaly v (deg) | |
|---|---|---|---|
| My Output | 0.01670 | 92.58 | 93.55 |
| Horizons | 0.01648 | 90.13 | 92.02 |
I’m going to assume that JPL is the gold standard! But because I’m following Meeus (Chap. 31) my value for M accords with the VSOP87 theory while JPL uses ICRF. A quick check with Mathematica shows M = 92.15. In any case, this isn’t bad for “armchair” computing on a personal laptop.
Sources
I am a software developer by trade and not a mathematician. So I was absolutely dependent on all three of these sources for my understanding of KE. Most of the trigonometry above is copied exactly from Smart and I retained his formula numbers for easy reference. If there is no formula number then you can certainly blame me rather than Smart for any errors. My task was largely to organize and make sense of the material for my own benefit and then use that understanding to implement the software solution.
Colwell, Peter. Solving Kepler’s Equation Over Three Centuries. Willmann-Bell. 1993.
Meeus, Jean. Astronomical Algorithms. 2nd Ed. Willmann-Bell. 1998.
Smart, W.M. Textbook on Spherical Astronomy. 6th Ed. Cambridge University Press. 1977.
Shout Outs
A thank you to Ketil Wright for pointing out equal sign typos in equations (63) and (66) and a place where it should have read “focus” (singular) instead of “foci” (plural).
| Angular momentum: Mass: Max radius: |
Introduction
The display above shows, from three different physical perspectives,the orbit of a low-mass test particle, the small red circle,around a non-rotating black hole (represented by a greycircle in the panel at the right, where the radius of the circle isthe black hole's gravitational radius, orevent horizon. Kepler's laws of planetary motion, grounded inNewton's theory of gravity, state that the orbit of a test particlearound a massive object is an ellipse with one focus at the centreof the massive object. But when gravitational fields are strong, asis the case for collapsed objects like neutron stars and blackholes, Newton's theory is inaccurate; calculations must be done usingEinstein's theory of General Relativity.
In Newtonian gravitation, an orbit is always an ellipse. As thegravitating body becomes more massive and the test particle orbits itmore closely, the speed of the particle in its orbit increases withoutbound, always balancing the gravitational force. For a blackhole, Newton's theory predicts orbital velocities greater than thespeed of light, but according to Einstein's Special Theory ofRelativity, no material object can achieve or exceed the speed of light.In strong gravitational fields, General Relativity predictsorbits drastically different from the ellipses of Kepler's laws.This page allows you to explore them.
The Orbit Plot
The panel at the right shows the test mass orbiting the black hole,viewed perpendicular to the plane of its orbit. The path of the orbit istraced by the green line. After a large number of orbits the displaywill get cluttered; just click the mouseanywhere in the right panel to erase the path and start over. Whenthe test mass reaches its greatest distance from the black hole, ayellow line is plotted from the centre of the black hole to thatpoint, the apastron of the orbit. In Newtonian gravity,the apastron remains fixed in space. The effects of General Relativitycause it to precess. You can see the degree of precession inthe displacement of successive yellow lines (precession can be morethan 360°; the yellow line only shows precession modulo onerevolution).
The Gravitational Effective-Potential
The panels at the left display the orbit in two more abstract ways.The Effective Potential plot at the top shows the positionof the test mass on the gravitational energy curve as it orbitsin and out. The summit on the left side of the curve is unique toGeneral Relativity—in Newtonian gravitation the curve rises withoutbound as the radius decreases, approaching infinity at zero. In Einstein'stheory, the inability of the particle to orbit at or above the speed of light creates a “pit in the potential” near the black hole.As the test mass approaches this summit, falling in from larger radiiwith greater and greater velocity, it will linger near the energypeak for an increasingly long time, while its continued angular motionwill result in more and more precession. If the particlepasses the energy peak and continues to lesser radii, towardthe left, its fate is sealed—it will fall into the black holeand be captured.
The Gravity Well
Spacetime around an isolated spherical non-rotating unchargedgravitating body is described by Schwarzschild Geometry, inwhich spacetime can be thought of as being bent by the presence ofmass. This creates a gravity well which extends to thesurface of the body or, in the case of a black hole, to oblivion. Thegravity well has the shape of a four-dimensional paraboloid ofrevolution, symmetrical about the central mass. Since few Webbrowsers are presently equipped with four-dimensional displaycapability, I've presented a two-dimensional slice through the gravitywell in the panel at the bottom left. Like the energy plot above, theleft side of the panel represents the centre of the black hole and theradius increases to the right. Notice that the test mass radius movesin lockstep on the two charts, as the radius varies on the orbit plotto their right.
The gravity well of a Schwarzschild black hole has a throatat a radius determined solely by its mass—that is the location of thehole's event horizon; any matter or energy which crosses thehorizon is captured. The throat is the leftmost point on the gravitywell curve, where the slope of the paraboloidal geometry becomesinfinite (vertical). With sufficient angular momentum, a particle canapproach the event horizon as closely as it wishes (assuming it issmall enough so it isn't torn apart by tidal forces), but it can nevercross the event horizon and return.
Hands On
By clicking in the various windows and changing values in the controlsat the bottom of the window you can explore different scenarios.To pause the simulation, press the Pause button at theright; pressing it again resumes the simulation. Click anywhere in the orbit plot at the right to clear the orbital trail andapastron markers when the screen becomes too cluttered. You can re-launchthe test particle at any given radius from the black hole (withthe same angular momentum) by clicking at the desired radius in eitherthe Effective Potential or Gravity Well windows. The green linein the Effective Potential plot indicates the energy minimum at which a stablecircular orbit exists for a particle of the given angular momentum.
The angular momentum is specified by the box at left in terms of theangular momentum per unit mass of the black hole, all ingeometric units—all of this is explained indetail below. What's important to note is that for orbits like thoseof planets in the Solar System, this number is huge; only in stronggravitational fields does it approach small values. If the angularmomentum is smaller than a critical value(, about 3.464 fora black hole of mass 1, measured in the same units), no stable orbitsexist; the particle lacks the angular momentum to avoid beingswallowed. When you enter a value smaller than this, notice how the trough inthe energy curve and the green line marking the stable circular orbitdisappear. Regardless of the radius, any particle you launch is doomedto fall into the hole.
The Mass box allows you to change the mass of the black hole,increasing the radius of its event horizon. Since the shape of theorbit is determined by the ratio of the angular momentum tothe mass, it's just as easy to leave the mass as 1 andchange the angular momentum. You can change the scale of allthe panels by entering a new value for the maximum radius; thisvalue becomes the rightmost point in the effective potentialand gravity well plots and the distance from the centre ofthe black hole to the edge of the orbit plot. When you changethe angular momentum or mass, the radius scale is automaticallyadjusted so the stable circular orbit (if any) is on screen.
Kepler, Newton, and Beyond
In the early 17th century, after years of tedious calculationand false starts, Johannes Kepler published his three laws ofplanetary motion:
- First law (1605): A planet's orbit about the Sun is an ellipse, with the Sun at one focus.
- Second law (1604): A line from the Sun to a planet sweeps out equal areas in equal times.
- Third law (1618): The square of the orbital period of a planet isproportional to the cube of the major axis of the orbit.
Kepler's discoveries about the behaviour of planets in theirorbits played an essential rôle in Isaac Newton's formulationof the law of universal gravitation in 1687. Newton'stheory showed the celestial bodies were governed by the samelaws as objects on Earth. The philosophical implications ofthis played as key a part in the Enlightenment as did thetheory itself in the subsequent development of physicsand astronomy.
While Kepler's laws applied only to the Sun and planets, Newton'suniversal theory allowed one to calculate the gravitational force andmotion of any bodies whatsoever. To be sure, when manybodies were involved and great accuracy was required, the calculationswerehorrificallycomplicated and tedious—so much so thatthose reared in the computer age may find it difficult toimagine embarking upon them armed with nothing but a table oflogarithms, pencil and paper, and the human mind. But performed theywere, with ever greater precision as astronomers made increasinglyaccurate observations. And those observations agreed perfectly withthe predictions of Newton's theory.
Well,… almost perfectly. After painstaking observationsof the planets and extensive calculation, astronomer Simon Newcombconcluded in 1898 that the orbit of Mercury was precessing 43arc-seconds per century more than could be explained by the influenceof the other planets. This is a tiny discrepancy, but furtherobservations and calculations confirmed Newcomb's—the discrepancy wasreal. Some suggested a still undiscovered planet closer to the Sunthan Mercury (and went so far as to name it, sight unseen,“Vulcan”),but no such planet was ever found, nor any other plausible explanationadvanced. For nearly twenty years Mercury's precession or “perihelionadvance” remained one of those nagging anomalies in the body ofscientific data that's trying to tell us something, if only we knewwhat.
In 1915, Albert Einstein's General Theory of Relativity extendedNewtonian gravitation theory, revealing previously unanticipated subtleties ofnature. And Einstein's theory explained the perihelion advance ofMercury. That tiny discrepancy in the orbit of Mercury wasactually the first evidence for what lay beyond Newtoniangravitation, the first step down a road that would lead tounderstanding black holes, gravitational radiation, and the source ofinertia, which remains a fertile ground for theoretical andexperimental physics a century thereafter.
Geometric Units
The force of gravity is so weak compared to the electromagneticforce which binds objects on the human scale, and the speed oflight so great compared to velocities with which we're familiar, thatcalculating the effects of general relativity, which involveboth the gravitational force and the speed of light, usingconventional units like grams, centimetres, and seconds usuallyresults in enormous or minuscule quantities cumbersome tomanipulate and difficult to understand intuitively.
If we're interested in the domain where general relativisticeffects are substantial, we're better off calculating with unitsscaled to the problem. A particularlyconvenient and elegant choice is the system of geometricunits, obtained by setting Newton's gravitationalconstant G, the speed of light c, and Boltzmann's constant k all equal to 1. Wecan then express any of the following units as a lengthin centimetres by multiplying by the following conversionfactors.
| Quantity | Unit | cm Equivalent |
|---|---|---|
| Time | second | 2.997930×1010 cm/sec |
| Mass | gram | 0.7425×10−28 cm/g |
| Energy | erg | 0.826×10−49 cm/erg |
| Electric charge | e | 1.381×10−28 cm/e |
| Temperature | ° Kelvin | 1.140×10−65 cm/°K |
Kepler Orbit Element
The enormous exponents make it evident thatthese units are far removed from our everyday experience.It would be absurd to tell somebody, “I'll call you backin 1.08×1014 centimetres”, but it is a perfectlyvalid way of saying “one hour”. The discussion that followsuses geometric units throughout, allowing us to treat mass,time, length, and energy without conversion factors. Toexpress a value calculated in geometric units back toconventional units, just divide by the value in the tableabove.
The Gravitational Effective-Potential
The gravitational effective-potential for a test particle orbitingin a Schwarzschild geometry is:
where isthe angular momentum per unit rest mass expressed in geometric units,M is the mass of the gravitating body, and r is theradius of the test particle from the centre of the body.
The radius of a particle from the centre of attraction evolves inproper time τ(time measured by a clock moving along with the particle)according to:
where is the potential energy of the test mass at infinity per rest mass.
Kepler Orbit Period
Angular motion about the centre of attraction is then:
while time, as measured by a distant observer advances according to:
and can be seen to slow down as the event horizon at the gravitationalradius is approached. At the gravitational radius of 2M time,as measured from far away, stops entirely so the particle never seemsto reach the event horizon. Proper time on the particle continues toadvance unabated; an observer on-board sails through the eventhorizon without a bump and continues toward the doom which awaitsat the central singularity.
Circular Orbits
Circular orbits are possible at maxima and minima of the effective-potential.Orbits at minima are stable, since a small displacement increases theenergy and thus creates a restoring force in the opposite direction.Orbits at maxima are unstable; the slightest displacement causes theparticle to either be sucked into the black hole or enter a highlyelliptical orbit around it.
To find the radius of possible circular orbits, differentiatethe gravitational effective-potential with respect to theradius r:
The minima and maxima of a function are at the zero crossings of itsderivative, so a little algebra gives the radii of possible circularorbits as:
The larger of these solutions is the stable circular orbit, while thesmaller is the unstable orbit at the maximum. For a black hole, thisradius will be outside the gravitational radius at 2M, whilefor any other object the radius will be less than the diameter ofthe body, indicating no such orbit exists. If the angularmomentum L² is less than 12M², no stable orbitexists; the object will impact the surface or, in the case of ablack hole, fall past the event horizon and be swallowed.
References
| Click on titles to order books on-line from |
- Gallmeier, Jonathan, Mark Loewe, and Donald W. Olson. “Precession and the Pulsar.” Sky & Telescope (September 1995): 86–88.
- A BASIC program which plots orbital paths in Schwarzschild geometry. The program uses different parameters to describe the orbit than those used here, and the program does not simulate orbits which result in capture or escape. This program can be downloaded from the Sky & Telescope Web site.
- Misner, Charles W., Kip S. Thorne, and John Archibald Wheeler.Gravitation.San Francisco: W. H. Freeman, 1973. ISBN 978-0-7167-0334-1.
- Chapter 25 thoroughly covers all aspects of motion in Schwarzschild geometry, both for test particles with mass and massless particles such as photons.
- Wheeler, John Archibald.A Journey into Gravity and Spacetime.New York: W. H. Freeman, 1990. ISBN 978-0-7167-5016-1.
- This book, part of the Scientific American Library series (but available separately), devotes chapter 10 to a less technical discussion of orbits in Schwarzschild spacetime. The “energy hill” on page 173 and the orbits plotted on page 176 provided the inspiration for this page.
Other Physics Resources at Fourmilab
Fourmilab Home Page
by John WalkerFebruary 1997
Update: December 1998
Kepler Orbital Period Equation
Update: June 2008Update: January 2017
